Význam metod verifikace a validace výsledků z CFD analýz při výpočtech vibrací vyvolaných prouděním pro návrh zařízení na výměnu tepla

Úvod a motivace

Jev vibrace vyvolané prouděním je znám několik staletí neřkuli tisíciletí. My Češi pak můžeme být právem hrdi na našeho fyzika, Vincence (Čenka) Strouhala, který se velkou měrou zasadil o pokrok na poli akustické fyziky. Jako první popsal závislosti frekvencí při odtrhávání vírů při obtékání tekutiny kolem kruhového profilu [1]. Význam tohoto poznatku je zásadní a to zejména pro zařízení na výměnu tepla, ve kterých dochází k obtékání teplosměnných ploch. Mezi nejběžnější teplosměnné plochy patří trubky, resp. trubkové svazky, nejčastěji právě s kruhovým profilem. Obecně platí fakt, že tepelný výkon je tím větší, čím lépe tekutina rozrušuje mezní vrstvu a homogenizuje tok u teplosměnných ploch. Toho bývá dosaženo například při použití trubek ve svazku v uspořádání 30° a 45°, přepážek pro usměrnění toku, zvýšení rychlostí pracovních médií, atd. Během návrhu zařízení pro daný tepelný výkon dochází při zmíněném zvyšování rychlosti ke zvyšování součinitele prostupu tepla a díky tomu je možné zmenšit teplosměnné plochy, tedy snížit počet trubek nebo zkrátit délku výměníku, což vede ke snížení investičních nákladů. Na druhé straně zvyšováním rychlosti proudění se zvyšují tlakové ztráty a tím i provozní náklady na dopravu pracovních médií.

Právě rychlost pracovní látky hraje klíčovou roli nejen pro návrh zařízení na výměnu tepla, ale i pro jejich životnost. Obecně lze říci, že při malých rychlostech může docházet k zanášení a malým tepelným výkonům, naopak při velkých rychlostech může docházet k vibracím a eroznímu opotřebení a ke vzrůstu tlakových ztrát, které prodražují chod těchto zařízení. Současný stav poznání stanovuje doporučená rozmezí rychlostí pro tekutiny v mezitrubkovém a trubkovém prostoru, které jsou uvedena v Tab. 1. Horní rychlostní mez je vztažena k možnosti vzniku vibrací, naopak dolní rychlostní mez ke vzniku zanášení [2].

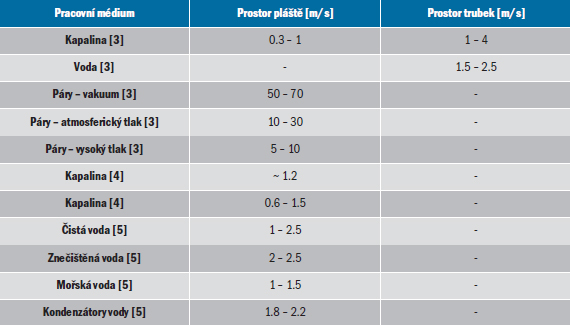
Tab. 1 – Doporučené meze rychlostí tekutin v trubkových výměnících tepla

Návrh trubkových výměníků tepla

Návrh výměníků tepla se provádí jak po stránce tepelně-hydraulické, tak i po stránce pevnostní. Součástí návrhu by bezpochyby mělo být i vyhodnocení míry zanášení a nebezpečí vibrací. Poddar a Polley [2] uvádí metodu, která na základě požadovaného tepelného výkonu a dalších parametrů umožňuje sestrojit grafické znázornění tlakových ztrát a zanášení pro různé délky a počty trubek zařízení. Cílem uvedené metody je identifikovat právě ty geometrie, které splňují následující omezení:

• Výměník je schopen přenášet požadovaný tepelný výkon.
• Tlaková ztráta v trubkovém prostoru nepřesahuje maximální doporučenou hodnotu.
• Tlaková ztráta v mezitrubkovém prostoru nepřesahuje maximální doporučenou hodnotu.
• Rychlost na trubkové i plášťové straně je menší než maximální hodnota a větší než minimální hodnota rychlosti.
• Délka trubek je menší než maximální dovolená hodnota.
• Průměr skořepiny je menší než maximální přípustná hodnota.

Obrázek 2 znázorňuje reálný návrh výměníku tepla podle grafické metody Poddara a Polleyho s následujícími parametry:

• Tepelný výkon výměníku = 1.33 MW;
• Vypočítané / dovolené tlakové ztráty vmezitrubkovém prostoru = 26.11 kPa/ 30 kPa;
• Vypočítané / dovolené tlakové ztráty v trubkovém prostoru = 12.56 kPa/ 30 kPa;
• Vnitřní průměr pláště = 650 mm;
• Rychlost vmezitrubkovém prostoru =0.29m/s;
• Rychlost v trubkovém prostoru = 0.46 m/s;
• Délka trubek = 5.5 m.

Oblast návrhu z obrázku 2 je definována křivkami teplosměnných ploch (resp. výkonu), tlakových ztrát v trubkovém a mezitrubkovém prostoru a limity doporučených rychlostí dle Tab. 1. Oblast zanášení je určena minimální rychlostí v trubkovém a mezitrubkovém prostoru, stejně tak oblast vibrací je určena maximální rychlostí v trubkovém a mezitrubkovém prostoru. Pro tento konkrétní případ lze považovat nejekonomičtější návrh v místě průniku křivky popisující teplosměnnou plochu a tlakovou ztrátu na straně trubek. Návrh pomocí metody Poddara a Polleyho byl konfrontován s klasickou metodou návrhu pomocí softwaru americké společnosti HTRI, výsledek z tohoto softwaru je v blízkosti nejekonomičtějšího návrhu na obrázku 2.

Verifikace a validace výsledků pro numerické analýzy

Před samotným popisem možných způsobů pro verifikaci a validaci výsledků získaných z numerických analýz proudění CFD (Computational Fluid Dynamics) je na místě popsat význam verifikace a validace z hlediska CFD:

• Verifikace ověřuje správnost programovací a výpočetní implementace konceptuálního modelu [6]. Stejně tak zkoumá použitelnost matematických modelů s přesnými analytickými výsledky. Mimo jiné verifikace ověřuje také chyby výpočtového programování.
• Validace posuzuje, zda výpočetní simulace souhlasí s fyzikální realitou. Stejně tak zkoumá korektnost modelů skrze porovnání s experimentálními výsledky.

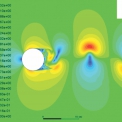
Při používání numerických analýz, jako je CFD, je dobrým zvykem ověřit a potvrdit výsledky analýz pomocí experimentálních nebo již známých a ověřených analytických výpočtů. Jak bylo uvedeno výše, cílem této práce je prozkoumání možností ověření a potvrzení CFD analýz a to konktrétně za pomocí Reynoldsova čísla, Strouhalova čísla, úhlu odtržení víru od trubky a tlakové distribuce na vnějším povrchu osamocené trubky. Přehled rychlostní distribuce v doméně je znázorněn na obrázku 1 pro Reynoldsovo číslo = 2191.

Okrajové podmínky

Pro zvolenou doménu s kruhovou trubkou byly zvoleny okrajové podmínky uvedené Tab. 2. V této tabulce jsou uvedeny parametry tří konfigurací, lišící se v Reynoldsových číslech, které byly řešeny v rámci této práce. Pro CFD analýzu byl použit 2D geometrický model s průměrem trubky 32 mm. Úloha byla řešena jako izotermní pro jednofázové proudění. Viskózní model DDES se stěnovou funkcí RANS Model – SST k-omega. Hodnota velikosti časového kroku (Δs) pro CFD analýzu z Tab. 2 je vypočtena v souladu s obecně známou Strouhalovou rovnicí, která popisuje vliv frekvencí odtrhávaných vírů v závislosti na rychlosti tekutiny a charakteristickém rozměru (průměru trubky) při ustáleném toku. Tato rovnice má mnoho modifikací. Jednou z těchto modifikací je vyjádření popsané rovnicí (1).

Rovnice (1) je používána pro určení životnosti víru, kde volitelná konstanta K určuje počet dělení v průběhu životnosti víru. Hodnota K má vliv na dobrý popis hodnot vztahujícím se k časově proměnným veličinám na stěně trubky (tlakový součinitel, součinitel vztlaku a odporu, atd.). V mnoha publikacích je jako dostatečně vyhovující volena hodnota K = 10. Uvedená hodnota však nemusí být vždy dostačující, jak se ukazuje například při popisu špiček vztlakových a odporových součinitelů. Menší hodnota K sice umožňuje zkrácení doby výpočtu, avšak snižuje přesnost výpočtu. Kromě toho menší časový krok, tj. větší K, zajišťuje lepší konvergenci CFD výpočtů. Z tohoto důvodu je hodnota K v provedených CFD výpočtech rovna 20.

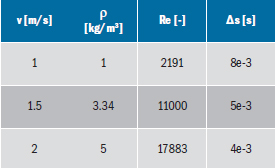
Tab. 2 – Vstupní data pro CFD analýzy

Verifikace a validace CFD analýz pomocí Strouhalova čísla

Vztah mezi Reynoldsovým a Strouhalovým číslem pro obtékanou trubku popsal v roce 1966 Lienhard. Závislost těchto dvou bezrozměrných čísel je znázorněna v Obrázek 3 pro hladký a hrubý povrch trubky. Do stejného grafu jsou zaneseny výsledky z CFD analýz pro tři výše zmíněné konfigurace vyjádřené hodnotami Reynoldsových čísel 2191, 11000 a 17883, klíčové výsledky jsou znázorněny v Tab. 3. Z obrázku 3 je zřejmé, že hodnoty Strouhalových čísel docela přesně odpovídají křivce s hladkým povrchem. V tomto grafu pak v roce 1967 Gregorig vymezil oblast s experimentálně prokazatelným výskytem vibrací [7]. Tato oblast je také znázorněna v obrázku 3.

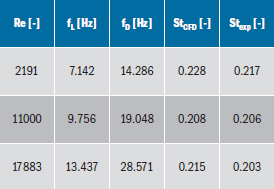
Tab. 3 – Klíčové výsledky z CFD analýz

Verifikace a validace CFD analýz pomocí úhlu odtržení víru

Další možnost verifikace a validace, využitou v tomto příspěvku, poskytuje úhel odtržení víru od trubky. Úhel odtržení od trubky vychází z experimentálně zjištěných dat v závislosti na velikosti Reynoldsova čísla, která jsou regresně proložena dvěma křivkami. Tyto křivky jsou popsány rovnicemi (2) a (3) [8].

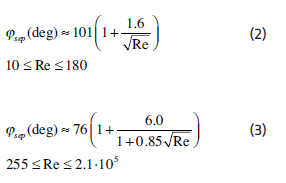
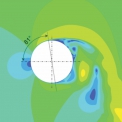
Dle rovnice (3) bylo pro Reynoldsovo číslo = 11000 dopočítáno hodnota úhlu odtržení víru, která je přibližně rovna hodnotě 81 °. Obrázek 4 znázorňuje distribuci rychlostního pole a úhel odtržení víru v konfiguraci toku pro stejné Reynoldsovo číslo. Z něj je patrné, že se experiment s CFD výpočtem shoduje.

Verifikace a validace CFD analýz pomocí rozložení tlakového koeficientu na trubce

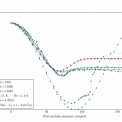
Poslední možností verifikace a validace vybranou pro tento příspěvek je využití rozložení tlakového součinitele na trubce. Toto rozložení je znázorněno na obrázku 5. Pro válcová tělesa jsou známy výsledky mnoha experimentálních měření tlakových distribucí při příčném obtékání. Vybrané hodnoty z experimentálního měření od Batchelora (pro Re = 11000) a Taniho (pro Re = 465000) jsou konfrontovány s vypočtenými hodnotami získanými pro Reynoldsova čísla = 2191, 11000 a 17883. Z obrázku 5 je zřejmé, že pro Re = 11000 se rozložení tlakové distribuce téměř shoduje.

Závěr

Hlavním cílem této práce bylo zdůraznění významu rychlosti pracovních médií při návrhu výměníků tepla jak z hlediska jejich tepelného výkonu, investičních a provozních nákladů, tak z hlediska doprovodných nežádoucích provozních jevů, jakými jsou například vibrace a zanášení. Dále pak zvážení potenciálu využití moderních numerických metod při studiu vibrací. Za tímto účelem je nutné verifikovat a validovat použité modely, tak aby jejich věrohodnost byla srovnatelná s výsledky experimentů. Tomu je věnována druhá část práce, konkrétně s využitím Strouhalova čísla, Reynoldsova čísla a tlakové distribuce kolem trubky. Za pomocí výše uvedených způsobů verifikace a validace bylo prokázáno, že takto ověřené CFD analýzy odpovídají naměřeným hodnotám a jsou tak použitelné pro další studium problematiky jako plnohodnotná náhrada za nákladné experimentální postupy.

Poděkování
Tento článek vznikl v rámci projektu NETME CENTRE PLUS (LO1202) za finanční podpory Ministerstva školství, mládeže a tělovýchovy v rámci Národního programu udržitelnosti I.

Literatura
[1] Č. STROUHAL, Akustika, Jednota českých matematiků, Praha, 1902
[2] T. K. PODDAR, G.T. POLLEY, Heat exchanger design through parameter plotting, Trans IChemE, Vol 74, Part A, November 1996
[3] R. K.SINNOTT, Chemical Engineering Design, Great Britain: Elsevier, 2005, ISBN 0-7506-6538-6
[4] J. H.LIENHARD, A Heat transfer textbook, Massachusetts, USA: Phlogiston Press, 2006, ISBN 0-1338-5089-7
[5] J. KADRNOŽKA, V. LIBICH, Parní turbíny a kondenzace, Brno, Vysoké učení technické, 1987
[6] AIAA Standards, Guide: Guide for the Verification and Validation of Computational Fluid Dynamics Simulation, American Institute of Aeronautics and Astronautics, 1998, eISBN 978-1-56347-285-5.
[7] R. GREGORIG, H.K. ANDRITZKY, P. GRASSMANN, A. KONIG, Vibration Criteria of a Tube in Crossflow (in German), Part I, Basic Mechanism, Chemie-Ing.-Techn., 39., 894-900 (1967)
[8] CH. DALTON, Fundamentals of Vortex-induced vibration, University of Houston

Importance of the method of verifying and validating the results of CFD analyses for calculating flow-induced vibration in the design of heat exchangers
Flow-induced vibration can cause major problems in heat transfer equipment as used in the energy industry, in particular heat exchangers and reactors. Nowadays, with the development of computer technology, computing methods based on numerical analysis are being more frequently used. Numerical analysis not only supplements commonly used analytical and empirical procedures, but often provide better and more accurate results. On the other hand, numerical analysis can be demanding for both computing time and the computing equipment itself and, ultimately, on the qualified operator. The results of these analyses may provide a more detailed description of physical occurrences. However, the veracity of these results to the real situation remains a problem.

Autoři

• Ing. Buzík Jiří
• Ing. Létal Tomáš Ph.D.
• doc. Ing. Jegla Zdeněk Ph.D.