Srovnání přístupů pro stanovení akustické rezonance

• Foto

Úvod a motivace

Součástí vibračních mechanismů je jev, který je známí jako akustická rezonance. Obecně lze říci, že vzniká především při proudění plynů. Jeho projevem je oscilace kolmá ke směru proudění a ke směru osy trubky. V případě, kdy vlastní akustická frekvence mezitrubkového prostoru dosáhne excitační frekvencí trubek, může dojít ke sjednocení a následné konverzi kinetické energie od proudící tekutiny do vln akustického tlaku. Akustická rezonance je způsobena buď vírovým uvolňováním, nebo turbulentní excitací mající frekvenci, která se shoduje s vlastní frekvencí prostoru, ve kterém proudí tekutina. Je doprovázena hlasitou akustickou emisí a dochází při ní k rychlému poškození struktury komponent. K akustické rezonanci může docházet nezávisle na mechanických vibracích trubek. [1], [2], [3]

Cílem příspěvku je srovnání analytického přístupu popsaného publikací TEMA [1] s numerickým  2D modelem pomocí CFD (computational fluid dynamics) a provedeným experimentem. TEMA [1] predikuje akustickou rezonanci za pomocí tří podmínek. Při splnění jedné z těchto podmínek by mělo dojít k akustické rezonanci. Pro porovnání bude dále popsána geometrie domény s trubkovým svazkem.

Současný stav poznání

TEMA [1] definuje výskyt akustické rezonance v případě, že je splněna jedna z následujících podmínek nerovnic (1), (2) a (3):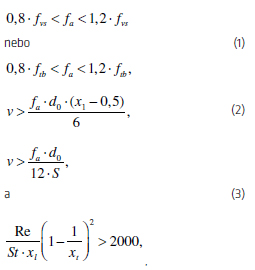



kde f_vs = frekvence vírového uvolňování (Hz),
f_a = akustická frekvence (Hz),
f_tb = frekvence turbulentní excitace (Hz),
d_o = průměr trubky (m),
x_l = poměr podélné rozteče k průměru trubky (-),
x_t = poměr příčné rozteče k průměru trubky (-),
S_t = Strouhalovo číslo (-),
R_e = Reynoldsovo číslo (-),
v = rychlost tekutiny (m/s).

VDI Heat Atlas [4] přistupuje k predikci akustické rezonance stejně jako publikace TEMA [1]. A to tak, že akustická rezonance nastává v případě, kdy dojde ke shodě frekvencí vírového uvolňování nebo frekvence turbulentní excitace s akustickou frekvencí. Stejně tak jako i v publikaci Tema, také VDI uvažuje 20% rezervu k akustické frekvenci, kde by mohlo docházet k frekvenčnímu sjednocení. Tato podmínka je znázorněna nerovnicí (1). Akustická rezonance závisí především na akustickém útlumu vzhledem k excitační energii od vírového uvolňování. Chen a Young [5] definují nerovnici (2) popisující charakter tlumení uvnitř trubkového svazku pro akustickou rezonanci. 

Heat Exchanger Design Handbook [6] přistupuje ke stanovení akustické frekvence pomocí tzv. stojaté vlny pro (n = 1, 2, 3, …) počet režimu, kterou přestavuje rovnice (4):

Proměnná C (m/s) vyjadřuje rychlost zvuku a je popsána rovnicí (5),

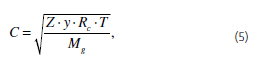
kde L_a = vzdálenost mezi stěnami kolmými ke směru toku (m),
Z = kompresibilní faktor (-),
R = molární plynová konstanta (J/(K·mol)),
T = absolutní teplota pracovního média (K),
γ = Poissonova konstanta (-),
Mg = molární hmotnost pracovního média (kg/mol).

Stejně tak Blevins [7] zavedl pojem hladina akustického tlaku (sound pressure level – SPL) při rezonanci. V případě rezonance lze stanovit velikost SPL dle rovnice (6). V případě, kdy SPL < 140 (dB), nebude docházet k poškození struktury komponent nebo jejich okolí:

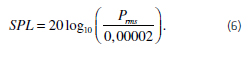
Okrajové podmínky

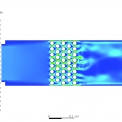
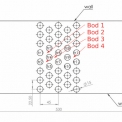
Jak bylo výše uvedeno, pro byla pro účely výpočtu vytvořena doména, která bude analyzována. Doména byla vybrána ve tvaru kvádru 180x180x500 mm, kde vstupní a výstupní prostor je odsazen o 15 mm z každé strany. Klíčové rozměry této domény v řezu jsou znázorněny na obrázku 1. Obrázek 1 znázorňuje doménu s trubkovým svazkem, na které byla prováděna 2D CFD analýza. Další, dosud nepopsané, okrajové podmínky jsou znázorněny v tabulce 1.

V tabulce 1 je zmíněn odhad Strouhalova čísla, který je odečten z obrázku 2. Obrázek 2 je znám jako Fitz-Hughova mapa pro trojúhelníkově uspořádané trubky [8], která je sestavena na základě experimentálního měření. Hodnota odečtená z Fitz-Hughovy mapy je znázorněna červenou tečkou na obrázku 2. Dle rovnice (7) stanovena velikost časového kroku na hodnotu 0,0013 sekund. Pro zaručení konvergence výpočtové úlohy, byla tato hodnota snížena na hodnotu 0,0001 sekundy.

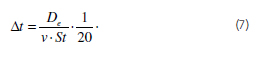
Porovnání výsledků analytického a numerického přístupu pro hodnocení akustické rezonance

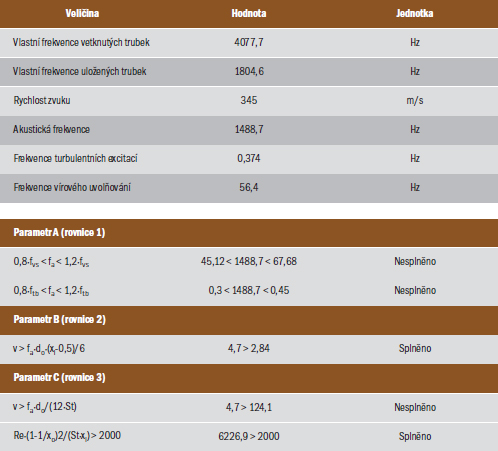
Jak bylo v úvodu zmíněno, cílem předkládaného článku je srovnání analytického a numerického přístupu pro hodnocení výskytu akustické vibrace, resp. akustické rezonance. Jako první bude přistoupeno k hodnocení výskytu akustické rezonance analytickým přístupem a to konkrétně metodikou popsanou v publikaci TEMA [1]. Tento přístup je popsán v kapitole 2. Výsledky z této analýzy jsou uvedeny v tabulce 2. TEMA [1] uvádí, že k akustické rezonanci může docházet, pokud je nějaký z parametrů A, B nebo C splněn. Z tabulky 2 je patrné, že parametr B (rovnice 2) a parametr C (rovnice 3) splňují parametr pro výskyt akustické rezonance pro výše uvedenou geometrii a okrajové podmínky.

Provedení numerické analýzy proudění uvnitř na vybrané geometrie umožňuje získat rychlostí a tlaková pole a tedy lokální závislosti veličin jako jsou frekvence vírového uvolňování, vztlakové a odporové součinitele, atd. Jako výpočtová doména byl vybrán dvourozměrný řez geometrií znázorněné na obrázku 1. Na tuto doménu byly aplikovány okrajové podmínky (tabulka 1) a následně byla provedená tranzientní 2D CFD analýza pomocí softwaru ANSYS Fluent. Jedním z výstupu této analýzy je rychlostní pole znázorněné na obrázku 3.

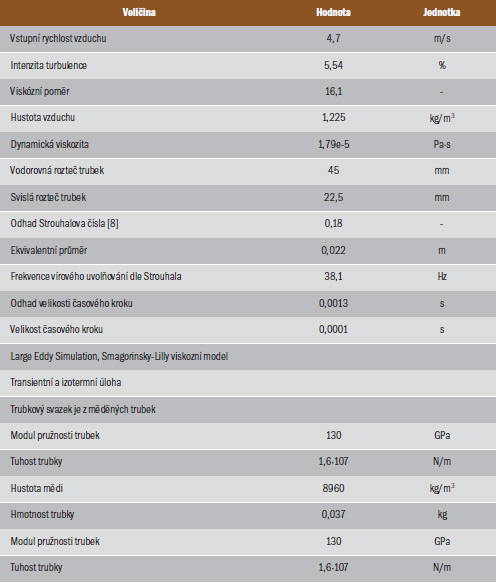
Tab. 1 – Tabulka okrajových podmínek

Jelikož se tento příspěvek zabývá srovnáním analytického a numerického přístupu je nezbytné pro toto srovnání vybrat právě ty veličiny, které mezi sebou korespondují. Mezi takové veličiny lze uvažovat především frekvence vírového uvolňování a turbulentních excitací z analytického přístupu a frekvence vírového uvolňování z numerického přístupu a velikost hladiny akustické intenzity získanou z numerického přístupu a její porovnání s hodnotou hladiny akustického tlaku, nad kterou bude docházet k poškození struktury komponent nebo jejího okolí. Tuto hladinu stanovil Blevins [7].

Tab. 2 – Výsledky hodnocení akustické rezonance analytickým přístupem

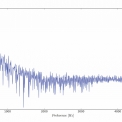
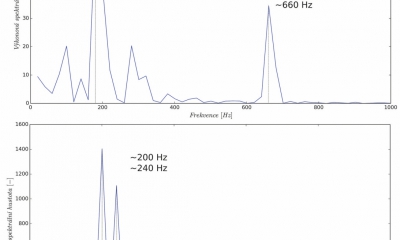
Z tabulky 1 a 2 lze vyčíst hodnoty analytické hodnoty a to především frekvenci vírového uvolňování pro trubkový svazek dle Strouhalova čísla 38,1 (Hz), tato hodnota by měla korespondovat s hodnotou frekvence vírového uvolňování 56,4 (Hz), což není splněno. Dále hodnotu frekvence turbulentní excitace 0,374 (Hz) a hodnotu akustické frekvence stojaté vlny v prvním tvaru 1488,7 (Hz). Pro zjištění frekvencí z numerické analýzy byla použita FFT analýza (rychlá Fourierova analýza) velikosti rychlosti ve směru proudění. Místa provedených sběru dat pro FFT analýzy jsou znázorněny na obrázku 1 jako bod 1 až 4. Výsledky z FFT analýzy z bodu 1 a bodu 3 jsou znázorněny na obrázku 4, kde se dominantní frekvence nachází při hodnotách přibližně 180 (Hz) a 660 (Hz) v případě bodu 1, resp. 200 (Hz) a 240 (Hz) v případě bodu 3. Tyto frekvence se velmi liší od frekvencí získaných z analytického výpočtu. Rozdíly ve frekvenčních hodnotách se dají vysvětlit několika důvody. Publikace Sound speed in a heat exchanger tube bank [9] je popisuje následovně:

• Frekvence vírového uvolňování v trubkovém svazku nelze měřit stejným způsobem jako pro jeden válec
• V průběhu měření může akustická vibrace/rezonance zasahovat do měření vírového uvolňování
• Do měření vstupují faktory jako vstupní intenzita turbulence nebo drsnost povrchu, které ovlivňují Strouhalovo číslo
• Některé frekvence vírového uvolňování jsou určeny z amplitudy kmitu trubky.

Výsledek závislosti hladiny akustického tlaku na frekvenci z CFD analýzy je znázorněn na obrázku 5. Z tohoto obrázku lze soudit, že nejvyšší hladina akustického tlaku vzniká při nízkých frekvencích. Po integraci všech hladin akustického tlaku skrze všechny frekvence odpovídá hladina akustického tlaku hodnotě 98.012 (dB) (při referenčním tlaku = 2e-5 Pa). Blevinsem [7] stanovil hodnoty hladiny akustického tlaku, pod níž nebude docházet k poškození struktury komponent nebo jejího okolí jak je uvedeno výše. Tento limit odpovídá hodnotě SPL < 140 (dB). Lze tedy konstatovat, že je zaznamenán výrazný nárůst hladiny akustického tlaku, nicméně k rezonanci dle prahové hodnoty by docházet nemělo.

Závěr

„Vibrace způsobené prouděním tekutiny jsou velmi komplexním problémem a současný stav poznání neumožňuje přesně definovat řešení tohoto problému. Kvůli komplexnosti problému TEMA negarantuje výskyt vibračních poškození.“ [1]

Výše uvedená publikace přímo navazuje na analytické výsledky uvedené v předkládaném článku. Metoda pro predikci vibrací popsaná v publikaci TEMA [1] umožňuje uživateli rychlou a relativně přesnou predikci vibrací vyvolaných prouděním. Bohužel neumožňuje predikovat případné lokální místa poškození, k tomu je zapotřebí pokročilejších výpočtových metod. Z tohoto hlediska se jeví využití numerických výpočtů jako vhodné východisko. Tyto výpočty poskytují přesné lokální výsledky, avšak na úkor výpočtového času a nezbytného ověření výsledků. Z těchto důvodů bylo přistoupeno ke konfrontaci právě výše zmíněných dvou metod a nalezení relevantních průsečíků, kterými se jeví právě frekvence vírového uvolňování a velikost hladiny akustické intenzity při dosažení rezonance.

Závěrem konfrontace numerického postupu s postupem analytickým lze konstatovat, že navzdory splnění podmínek popsaných metodikou TEMA [1], nebude v doméně docházet k akustické rezonanci. Na druhou stranu lze předpokládat, že při zvýšení vstupní rychlosti proudu by se bezpochyby akustická rezonance mohla vyskytnout.

Jelikož lze předpokládat, že pohyb trubky bude velkou měrou ovlivňovat akustickou emisi, jako budoucí práce se jeví kombinace akustické numerické analýzy s numerickou analýzou popisující interakci tekutiny a struktury. Jako vhodné východisko se jeví použití uživatelem definované funkce (UDF), která zabezpečuje pohyb vybraných objektů, kterým jsou definovány strukturální parametry, jako jsou například tuhost, hmotnost, moment setrvačnosti a jiné.

Poděkování
Tento článek vznikl v rámci projektu NETME CENTRE PLUS (LO1202) za finanční podpory Ministerstva školství, mládeže a tělovýchovy v rámci Národního programu udržitelnosti I.

Literatura
[1] TEMA. Standards of the tubular exchanger manufacturers association. 9th ed. B.m.: Tubular Exchanger Manufacturers Association. 2007.
[2] BLAKE, W. K. Mechanics of Flow-Induced Sound and Vibration. Orlando, Florida: Academic Press Inc., 1986. ISBN 0-12-103501-8.
[3] HALLE, H., J. M. CHENOWETH a M. W. WAMBSGANSS. DOE/ANL/HTRI Heat Exchanger Tube Vibration Data Bank. B.m.: Argonne Natl. Lab. Tech. Memo, 1980.
[4] VDI GESELLSCHAFT. VDI Heat Atlas. 2nd vyd. B.m.: Springer, 2010. ISBN 978-3-540-79999-3.
[5] CHEN, S. S. Fluid damping and fluid stuffiness of a tube row in cross-flow. ASME Journal of Pressure Vessel Technology. nedatováno, (Vol. 116), 370–383.
[6] THULUKKANAM, Kuppan. Heat Exchanger Design Handbook. 2nd. Boca Raton: CRC Press, Taylor & Francis Group, 2013. ISBN 978-1-4398-4213-3.
[7] BLEVINS, R. D. Flow Induced Vibration. 2nd vyd. 2001. ISBN 978-0-442-20651-2.
[8] FITZ-HUGH, J. S. Flow-induced Vibration in Heat Exchnager. Proc. Int. Sym. on Vibration Problems in Industry. 1973, 427.
[9] CHEN, Shoei-Sheng. Flow-induced vibration of circular cylindrical structures. ANL-85-51. Illinois: Argon National Laboratory. 1985.

Autoři

• Ing. Buzík Jiří
• Ing. Létal Tomáš Ph.D.
• Ing. Lošák Pavel Ph.D.
• Ing. Pernica Marek
• Ing. Naď Martin